
找答案
首页
【简答题】
设矩阵
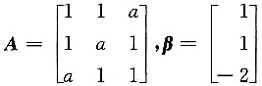 ,已知线性方程组AX=β有解但不唯一.试求: 正交矩阵Q,使Q T AQ为对角矩阵.
,已知线性方程组AX=β有解但不唯一.试求: 正交矩阵Q,使Q T AQ为对角矩阵.
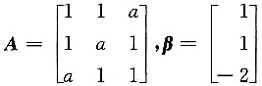 ,已知线性方程组AX=β有解但不唯一.试求: 正交矩阵Q,使Q T AQ为对角矩阵.
,已知线性方程组AX=β有解但不唯一.试求: 正交矩阵Q,使Q T AQ为对角矩阵.参考答案:
登录免费查看参考答案
参考解析:
登录免费查看参考解析
知识点:
登录免费查看知识点
答题技巧:
登录免费查看答题技巧
被用于:
暂无被用于


刷刷题刷刷变学霸
相关题目:
【单选题】设 是 矩阵, 是 矩阵,则线性方程组 【 】
【单选题】以下哪个是线性方程组\(\begin{pmatrix} 1 & -1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{pmatrix} \mathbf{x} = 0\)的解
【单选题】对三对角矩阵A采用压缩存储的方法将所有非零元素存放于一个一维数组B[3n-2]中,某非零元素aij在B中位置是____________。
【单选题】设A为m×n矩阵,B为n×m矩阵,则线性方程组(AB)x=0( )
【简答题】设Ax=0是含有n个未知量m个方程的线性方程组,且n>m,则Ax=0有______解。
【判断题】复对角矩阵diag{-1,2,3}与复对角矩阵diag{-1,-2,3}合同。
【单选题】已知线性方程组\[\left\{ \begin{array}{l} {x_1} + {x_2} + {x_3} + {x_4} = 0\\ {x_2} + 2{x_3} + 2{x_4} = 1\\ - {x_2} + (a - 3){x_3} - 2{x_4} = b\\ 3{x_1} + 2{x_2} + {x_3} + a{x_4} = - 1 \end{array} \right.\]若该...
【简答题】设分块矩阵 是正交矩阵,其中A,C分别为m,n阶方阵.证明:A,C均为正交矩阵,且B=O.设分块矩阵m*n是正交矩阵,其中A,C分别为m,n阶方阵.证明:A,C均为正交矩阵,且B=O.
【判断题】正交矩阵的行列式一定为1
【单选题】下列矩阵中为正交矩阵的是()。

刷刷题刷刷变学霸