
找答案
首页>初中数学>二次函数的定义考试题目
【简答题】
在平面直角坐标系中, O是坐标原点,直角梯形 AOCD的顶点 A的坐标为 (0,
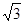 ),点 D的坐标为(1,
),点 D的坐标为(1,
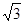 ),点 C在
),点 C在
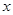 轴的正半轴上,过点 O且以点 D为顶点的抛物线经过点 C,点 P为 CD的中点.
轴的正半轴上,过点 O且以点 D为顶点的抛物线经过点 C,点 P为 CD的中点.
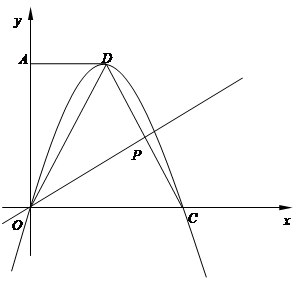 (1)求抛物线的解析式及点 P的坐标; (2) 在
(1)求抛物线的解析式及点 P的坐标; (2) 在
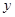 轴右侧的抛物线上是否存在点 Q,使以 Q为圆心的圆同时与
轴右侧的抛物线上是否存在点 Q,使以 Q为圆心的圆同时与
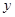 轴、直线 OP相切.若存在,请求出满足条件的点 Q的坐标;若不存在,请说明理由; (3)点 M为线段 OP上一动点(不与 O点重合),过点 O、 M、 D的圆与
轴、直线 OP相切.若存在,请求出满足条件的点 Q的坐标;若不存在,请说明理由; (3)点 M为线段 OP上一动点(不与 O点重合),过点 O、 M、 D的圆与
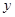 轴的正半轴交于点 N.求证: OM+ ON为定值. (4)在
轴的正半轴交于点 N.求证: OM+ ON为定值. (4)在
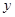 轴上找一点H,使∠PHD最大.试求出点H的坐标.
轴上找一点H,使∠PHD最大.试求出点H的坐标.
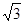 ),点 D的坐标为(1,
),点 D的坐标为(1,
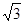 ),点 C在
),点 C在
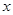 轴的正半轴上,过点 O且以点 D为顶点的抛物线经过点 C,点 P为 CD的中点.
轴的正半轴上,过点 O且以点 D为顶点的抛物线经过点 C,点 P为 CD的中点.
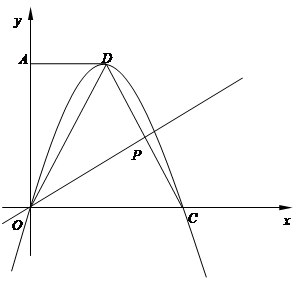 (1)求抛物线的解析式及点 P的坐标; (2) 在
(1)求抛物线的解析式及点 P的坐标; (2) 在
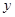 轴右侧的抛物线上是否存在点 Q,使以 Q为圆心的圆同时与
轴右侧的抛物线上是否存在点 Q,使以 Q为圆心的圆同时与
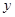 轴、直线 OP相切.若存在,请求出满足条件的点 Q的坐标;若不存在,请说明理由; (3)点 M为线段 OP上一动点(不与 O点重合),过点 O、 M、 D的圆与
轴、直线 OP相切.若存在,请求出满足条件的点 Q的坐标;若不存在,请说明理由; (3)点 M为线段 OP上一动点(不与 O点重合),过点 O、 M、 D的圆与
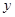 轴的正半轴交于点 N.求证: OM+ ON为定值. (4)在
轴的正半轴交于点 N.求证: OM+ ON为定值. (4)在
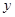 轴上找一点H,使∠PHD最大.试求出点H的坐标.
轴上找一点H,使∠PHD最大.试求出点H的坐标.参考答案:
登录免费查看参考答案
参考解析:
登录免费查看参考解析
知识点:
登录免费查看知识点
答题技巧:
登录免费查看答题技巧
被用于:
暂无被用于


刷刷题刷刷变学霸
相关题目:
【简答题】(本小题满分14分) 在直角坐标系 中,以 为极点, 轴的正半轴为极轴建立极坐标系.己知圆 的圆心的 极坐标为 半径为 ,直线 的参数方程为 为参数) (Ⅰ)求圆C的极坐标方程;直线 的普通方程; (Ⅱ)若圆C和直线 相交于A,B两点,求线段AB的长.
【简答题】已知抛物线C:y2=x,F为抛物线C的焦点,O为坐标原点,则在抛物线C上且满足△OFP为等腰直角三角形的点P的个数为( ) A.2 B.4 C.2或4 D.P点不存在
【简答题】已知:在直角坐标系中,A、B两点是抛物线y=x2-(m-3)x-m与x轴的交点(A在B的右侧),x1、x2分别是A、B两点的横坐标,且|x1-x2|=3.(1)当m>0时,求抛物线的解析式.(2)如果(1)中所求的抛物线与y轴交于点C,问y轴上是否存在点D(不含与C重合的点),使得以D、O、A为顶点的三角形与△AOC相似?若存在,请求出D点的坐标;若不存在,请说明理由.(3)一次函数y=kx+b的...
【简答题】在平面直角坐标系内,下列各点中在第二象限的点是( )
【简答题】平面直角坐标系下,A点到x轴的距离为2,到y轴的距离为4,且在x轴上方和y轴的左侧,则A点的坐标是______________.
【简答题】已知抛物线y 2 =2 p x( p >0)的焦点为F,直线L:2 p x+3y= p 2 - 。 ⑴当p为何值时,焦点F到直线L的距离最大; ⑵在第⑴题下,又若抛物线与直线L相交于A、B两点。求△ABF的面积。
【简答题】抛物线y=2x 2 -4x+9的对称轴是直线______.
【单选题】在测量平面直角坐标系中,第IV象限中的坐标增量为()
【简答题】如图,在直角坐标系中,已知点A(3,0),B(-3,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.(1)若抛物线y=13x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;(2)在(1)中的抛物线的对称轴上求一点P,使得△PBD的周长最小;(3)设Q为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边...
【单选题】在平面直角坐标系中,位于第二象限的点是( )

刷刷题刷刷变学霸