
找答案
首页>高中数学>数学归纳法证明不等式考试题目
【简答题】
(13分)
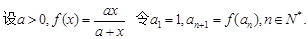 (1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;
(1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;
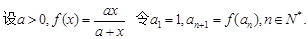 (1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;
(1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;参考答案:
登录免费查看参考答案
参考解析:
登录免费查看参考解析
知识点:
登录免费查看知识点
答题技巧:
登录免费查看答题技巧
被用于:
暂无被用于


刷刷题刷刷变学霸
相关题目:
【简答题】147归纳法是由一般到个别的思维方法。
【判断题】汇集法、归纳法、对比法、化小法属于对信息资料进行定性加工的方法。
【单选题】利用数学归纳法证明不等式1n+1+1n+2+…+1n+n>12(n>1,n?N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果为( )
【简答题】(12分)用数学归纳法证明等式对所以n∈N*均成立.
【简答题】.数列{a }满足S = 2n-a , n∈N ⑴计算a 、a 、a 、a ,并由此猜想通项公式a (2)用数字归纳法证明(1)中的猜想.
【简答题】已知点Pn(an,bn)(n∈N*)都在直线l:y=2x+2上,P1为直线l与x轴的交点,数列{an}成等差数列,公差为1.(Ⅰ)求数列{an},{bn}的通项公式;(Ⅱ)若f(n)=an,n为奇数bn,n为偶数问是否存在k∈N*,使得f(k+5)=2f(k)-5成立?若存在,求出k的值,若不存在,说明理由;(Ⅲ)求证:1|p1p2|2+1|p1p3|2+…+1|p1pn|2<25(n≥2,n∈N...
【简答题】已知数列{an}满足下列条件:a1=1,a2=r(r>0),且数列{anan+1}是一个以q(q>0)为公比的等比数列.设bn=a2n-1+a2n(n∈N*),Sn=b1+b2+…+bn.(1)求数列{bn}的通项公式bn;(2)求limn→∞1sn.
【单选题】儿童归纳图书内容的“一段话归纳法”一般适合于()的儿童使用。
【判断题】通过科学归纳法得出的结论比通过简单枚举归纳推理得出的结论更可靠。
【简答题】(13分) (1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;

刷刷题刷刷变学霸